저번 시간에는 비선형 서포트 벡터 머신(SVM) 분류기의 기본적인 개념과 사용법을 살펴보았다.
이번시간에는 SVM 분류가 아닌 SVM 회귀에 대해 알아보도록 하자.
SVM 회귀란?
SVM 회귀에 대해 알아보기 전에 SVM 분류가 어떤 식으로 동작하는지 살펴봤던 기억을 떠올릴 필요가 있다.
SVM 분류는 아래처럼 기준선과 샘플(서포트 벡터) 간의 거리(마진)가 최대가 되도록 하며, 기준선과 마진 사이에 샘플이 최대한 적게 들어가도록(마진 오류가 적도록) 선을 긋는 것이다.
[그림-1] SVM 선형 분류기
선형 SVM분류기의 경우, 기준선과 각 클래스 간의 거리(margin)가 가장 크도록 선을 긋는다. 그래서 라지 마진 분류(large margin classification)라고 불린다.
회귀는 분류와 같이 기준선과 샘플 간의 거리(마진)는 최대한으로 한다.
하지만, 분류와 달리 마진 내에 샘플들이 많이 들어가도록 하며 기준선을 긋는다는 차이가 존재한다.
아래의 선형 데이터셋 예제로 SVM 회귀가 어떻게 동작하는지 살펴보도록 하자.
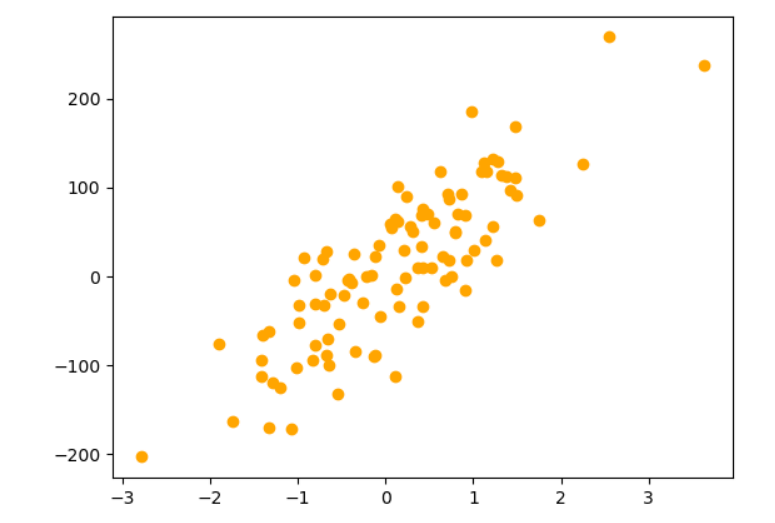
[그림 1]을 보면 선형적으로 증가하는 데이터셋이 만들어진 것을 확인할 수 있다.
이 데이터셋을 가지고 마진의 폭(epsilon)이 100인 선형 SVM 회귀모델을 만들어보도록 하자.

[그림 2]를 보면 마진의 폭이 100인 선형 SVM 회귀모델이 만들어진 것을 확인이 가능하다.
그렇다면 [그림 1]처럼 선형적인 데이터가 아니라 [그림 3-1]처럼 비선형적인 특성을 지닌 데이터는 어떻게 해야 하는가?

비선형 SVM 분류 때와 마찬가지로 커널함수를 사용하면 된다.
2차식의 다항식 커널함수를 사용한 결과 [그림 3-2]과 같은 결과를 얻을 수 있다. 확인해 보면 모델이 잘 만들어진 것을 확인이 가능하다.

SVM 회귀 사용하기
선형 SVM 회귀
선형 SVM 회귀는 sklearn.svm.LinearSVR()으로 회귀 모델을 만들 수 있다.
from sklearn.svm import LinearSVR
import numpy as np
from sklearn.datasets import make_regression
#훈련 샘플 생성
X,y = make_regression(n_samples = 100, n_features = 1, noise = 50, random_state = 2021)
#모델 불러오기 및 학습
svr_model = LinearSVR(epsilon=100)
svr_model.fit(X,y)
#시각화
xline = np.linspace(X.min(),X.max(),num=100)
xline = xline.reshape(100,1)
y_pred = svr_model.predict(xline)
plt.scatter(X,y,color="orange")
plt.plot(xline,y_pred,color="red")
plt.plot(xline,y_pred+100,"r--")
plt.plot(xline,y_pred-100,"r--")
파라미터
| epsilon | 도로의 폭. |
| tol | 중지 기준에 대한 허용 오차. |
| C | 오류를 얼마나 허용할 지에 대한 수치. C가 클수록 오류를 적게 허용하고, 낮을수록 오류를 많이 허용한다. (규제항) |
| random_state | 데이터를 섞을 때 사용할 난수를 만드는 시드값. 미지정시 기본적으로 시스템이 알아서 섞는다. |
| max_iter | 최대 반복 횟수. 기본은 1000이다. |
비선형 SVM 회귀
비선형 SVM 회귀의 경우 sklearn.svm.SVR()을 통해 모델을 만들 수 있다.
from sklearn.svm import SVR
import numpy as np
#random seed 결정
np.random.seed(2021)
#훈련 데이터셋 만들기
m = 100
X2 = 2 * np.random.rand(m, 1) - 1
y2 = (0.2 + 0.1 * X2 + 0.5 * X2**2 + np.random.randn(m, 1)/10).ravel()
#모델 만들기 및 학습
svr_model2 = SVR(kernel="poly", degree=2, C=100, epsilon=0.1, gamma="scale")
svr_model2.fit(X2,y2)
y_pred2 = svr_model2.predict(xline)
#모델 시각화
plt.figure(figsize=(10,4))
plt.subplot(1,2,1)
plt.scatter(X2,y2,color="orange")
plt.subplot(1,2,2)
plt.scatter(X2,y2,color="orange")
plt.plot(xline,y_pred2,color="red")
plt.plot(xline,y_pred2+0.1,"r--")
plt.plot(xline,y_pred2-0.1,"r--")
plt.axis([-1,1,0,1])
파라미터
| epsilon | 도로의 폭. |
| tol | 중지 기준에 대한 허용 오차. |
| C | 오류를 얼마나 허용할 지에 대한 수치. C가 클수록 오류를 적게 허용하고, 낮을수록 오류를 많이 허용한다. (규제항) |
| random_state | 데이터를 섞을 때 사용할 난수를 만드는 시드값. 미지정시 기본적으로 시스템이 알아서 섞는다. |
| max_iter | 최대 반복 횟수. 기본은 1000이다. |
참조
Geron Aurelien, 박해선 역, 핸즈온 머신러닝, 한빛미디어, 2020
https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVR.html
sklearn.svm.SVR
Examples using sklearn.svm.SVR: Prediction Latency Prediction Latency Comparison of kernel ridge regression and SVR Comparison of kernel ridge regression and SVR Support Vector Regression (SVR) usi...
scikit-learn.org
https://scikit-learn.org/stable/modules/generated/sklearn.svm.LinearSVR.html
sklearn.svm.LinearSVR
scikit-learn.org
'수업내용정리 > 인공지능' 카테고리의 다른 글
| [SckitLearn]앙상블 학습의 개념과 사용법(2)_배깅, 페이스팅 방식 (0) | 2023.02.18 |
|---|---|
| [SckitLearn]앙상블 학습의 개념과 사용법(1)_투표방식 (0) | 2023.02.17 |
| [SckitLearn]지도학습 알고리즘(3)_비선형 SVM 분류기의 특징과 사용법 (0) | 2023.02.14 |
| [SckitLearn]지도학습 알고리즘(2)_선형 SVM 분류기의 특징과 사용법 (0) | 2023.02.13 |
| [SckitLearn]지도학습 알고리즘(1)_의사결정트리의 특징과 사용법 (0) | 2023.02.11 |




